🛠️ Simplex Solver - App de escritorio

Core Solver y Funcionalidad

El corazón del proyecto utiliza el potente módulo scipy.optimize.linprog para proporcionar soluciones precisas de programación lineal. Maneja de forma robusta:

• Objetivos de Maximización y Minimización.
• Restricciones de Desigualdad \(\le, \ge\).
• Restricciones de Igualdad \(=\).
• Conversión automática de Variables Libres (sin restricción de no negatividad).

Interfaces de Usuario Avanzadas

1. Domain Specific Languages (DSLs)

Define problemas de optimización de forma programática o legible por humanos:

• String-based DSL: Para cargar problemas desde archivos .lp o directamente desde una cadena de texto en un formato estándar.
• Pythonic DSL: Una sintaxis elegante, inspirada en librerías matemáticas, que utiliza objetos y operadores de Python para construir el modelo de forma nativa.

2. Interfaz Gráfica (GUI) - PySide6

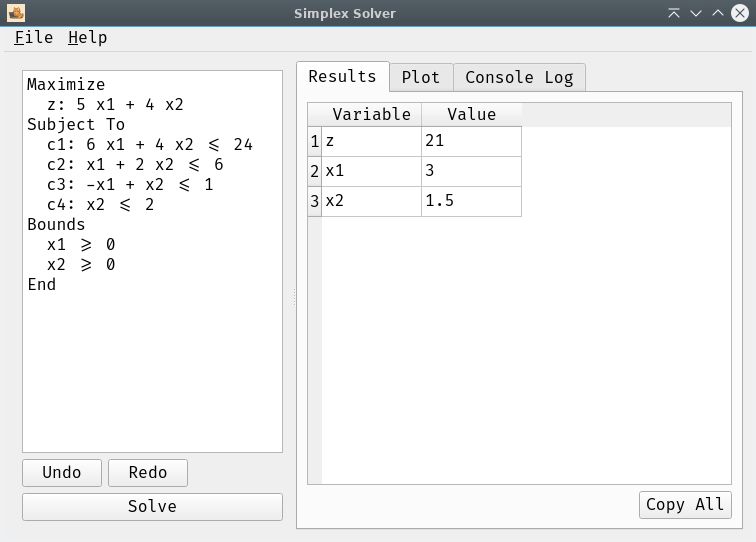
Una aplicación de escritorio completa construida con PySide6 (Qt) que ofrece una experiencia interactiva. Incluye editor, tabla de resultados y una consola de registro.

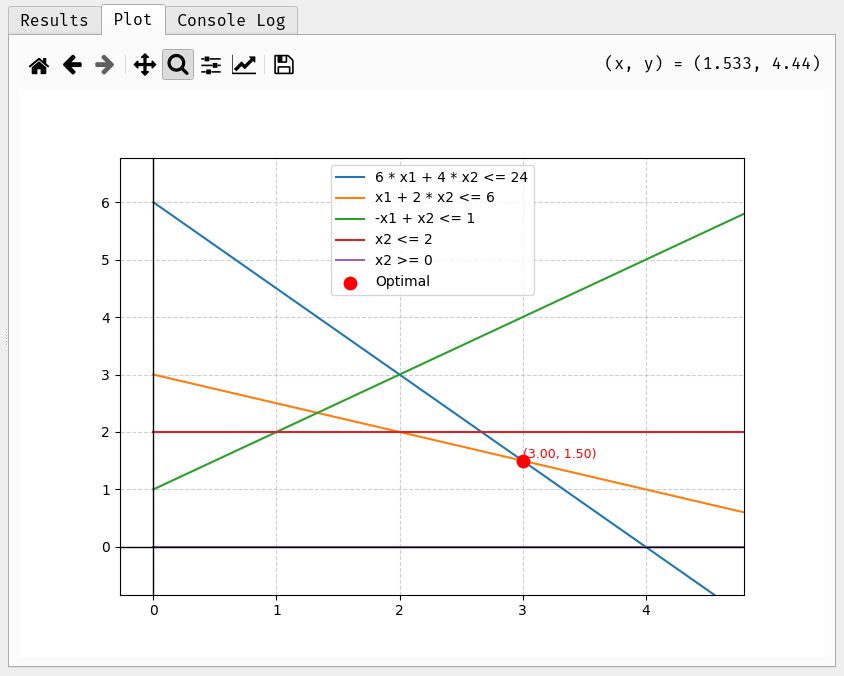
• Visualización Gráfica: Muestra la región factible y el punto óptimo para problemas de 2 variables.
• UI Responsiva: El solver corre en un hilo separado para evitar el congelamiento de la aplicación.

Ejemplo Práctico: Maximización de Ganancias

El siguiente ejemplo de optimización (productos A y B) se define de forma concisa utilizando el String-based DSL, que lee un formato similar a un archivo .lp tradicional:

from dsl import DSL
problema_lp = DSL("""
MAXIMIZE
    Z = 3*A + 4*B
SUBJECT TO
    2*A + 3*B <= 100
    1*A + 2*B <= 80
BOUNDS
    A >= 0
    B >= 0
""")
# 2*A + 3*B <= 100 # Horas de trabajo
# 1*A + 2*B <= 80 # Materia prima
solver = problema_lp.to_simplex()
solver.solve_problem()
solver.show_results()
# Solución óptima: A=20, B=30, Z_max = $180

Instalación y Uso Rápido

Instalación de Dependencias

Después de clonar el repositorio, usa pip para instalar todo lo necesario:

git clone https://github.com/xeland314/simplex.git
cd simplex
pip install -r requirements.txt

Lanzamiento de Interfaces

Ejecuta tu interfaz preferida con un solo comando:

• GUI (Aplicación de Escritorio):

python app.py

bashCopiar
• Command Line (CLI) Interactivo:

python simplex.py

bashCopiar